Dlaczego Jastrząb zawiódł? Część II

Druga część artykułu przybliżąjącego rozwój polskiego samolotu PZL50 Jastrząb.


PŁAT

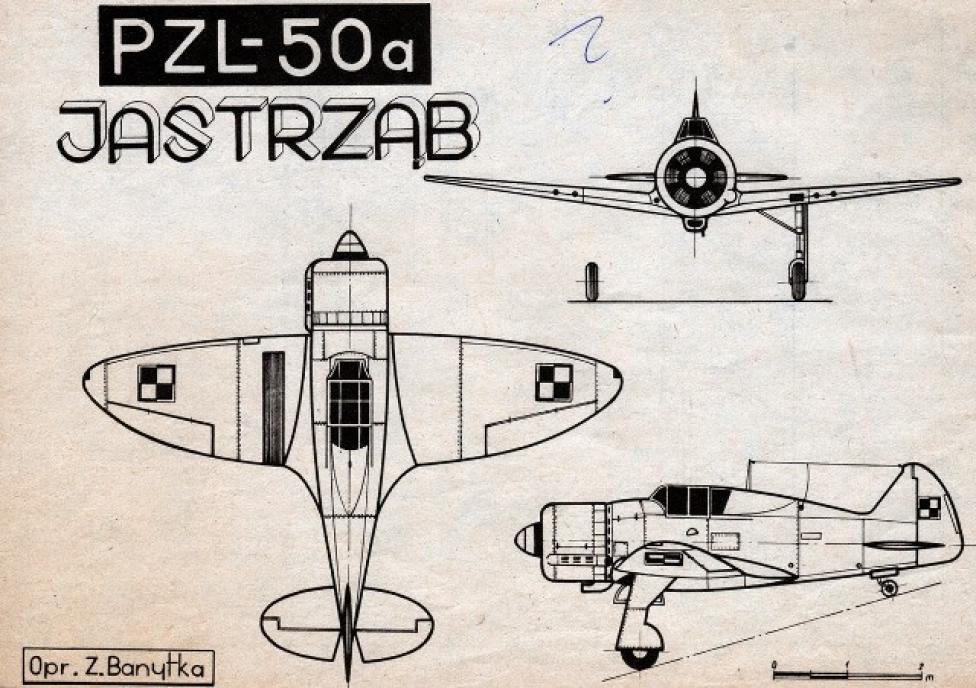
Fotografia widoczna poniżej przedstawia szczegóły konstrukcji kadłuba i centropłata. Na zdjęciu brakuje zewnętrznych części skrzydeł, zatem łatwo rozpoznać profil I.A.W. - 743. Samolot posiadał płat o obrysie eliptycznym. Poczynając od najstarszych rysunków z czasów wojny do dziś, powstało wiele wersji wyglądu skrzydeł. Najstarsza jest bodaj autorstwa inż. Głębockiego z 1941 roku opublikowana przez J.B. Cynka. Skrzydła bardzo różnią się od tych prezentowanych w późniejszych rysunkach. Uwagę zwracają ostro wycięte końcówki skrzydeł oraz duże wydłużenie. Z rysunków zamieszczonych w książce A. Morgały wyłania się samolot o zwartej sylwetce, wyposażony w skrzydła o ładnym eliptycznym obrysie i niewielkim wydłużeniu, stateczniki również na bazie elipsy dodają maszynie lotności i elegancji. Rysunki A. Glassa prezentują skrzydła o większym wydłużeniu i prostej krawędzi natarcia oraz trapezowy statecznik poziomy o skośnej krawędzi i zaokrąglonych końcówkach. W najnowszym wydawnictwie A. Morgała prezentuje bardzo zbliżoną sylwetę samolotu, co ciekawe pozbawioną zastrzałów pod statecznikiem poziomym.


Z tabeli nr 1 wynika, że Cx min płata umożliwia rozwijanie dużych prędkości lotu. Osiągnięcie wyższych prędkości było możliwe pod warunkiem modyfikacji skrzydeł. Samolot dysponujący mocą 840 KM i śmigłem o sprawności 0,85 na wysokości 4400 m osiągnąłby prędkość około 508 km/h przy Cx wynoszącym 0,03. Niewiele wiemy o usterkach płata, które trapiły prototypy Jastrzębia. Większość autorów podaje, że głęboka modernizacja samolotu miała polegać na powiększeniu zewnętrznych części płata do rozpiętości wynoszącej około 12,5 m, co dałoby powierzchnię nośną około 19 m2. Z obliczeń wynika jednak, że osiągnięcie prędkości 500 km/h przy tej powierzchni skrzydeł byłoby niemożliwe. Jerzy Gruszczyński dodaje, że nowy płat miał zapewnić maszynie lepsze własności lotne poprzez skręcenie aerodynamiczne zewnętrznych części płata oraz modyfikację przejścia kadłub-skrzydło. Zdaniem A. Glassa wprowadzenie tych zmian wiązało się z odejściem od koncepcji myśliwca pościgowego w stronę przechwytującego. Naszym zdaniem modernizacja płata wynikała z dwóch powodów.

Po pierwsze konstrukcja płata oparta na kesonie dwuobwodowym Jakimiuka miała wady w postaci zbyt dużego ciężaru i nierównej powierzchni dolnej generującej duży opór. Po drugie małe wydłużenie płata powodowało duży opór indukowany, który powiększał się podczas zakrętów na dużych kątach natarcia uniemożliwiając walkę powietrzną. Prototyp myśliwca rozwijający prędkość 430 km/h w 1939 roku to anachronizm. Nazwanie go przechwytującym czy pościgowym jest jedynie grą słów. Prędkość maksymalna nie może być jednak fetyszem. Na początku wojny zwrotnemu i nieźle uzbrojonemu myśliwcowi wystarczyłby zakres prędkości od 400 km/h przy powierzchni ziemi do 460 - 480 km/h na wysokości powyżej 4000 m.

Duży wpływ na wartość oporu płata ma niestaranne wykonanie lub niezbyt dopracowana technologia. Dwuobwodowy keson płata składał się z trzech ścianek pionowych, do których od spodu za pomocą śrub z nakrętkami kotwicznymi przykręcano panele spodnie, łącząc ich krawędzie listewkami z zębatymi wypustkami z jednej strony, z drugiej zaś z trapezowymi rowkami, co tworzyło rodzaj zamków. Pokrycie górne nitowano do ścianek pionowych. Rozwiązanie to było zbyt ciężkie i niedoskonałe technicznie. Dawało nierówną powierzchnię z wystającymi nakrętkami, wypukłymi brzegami listewek, którą z punktu widzenia aerodynamiki można określić jako chropowatą. Określenie to miało niewiele wspólnego z dotykiem i należy je wyjaśniać w oparciu o zjawiska aerodynamiczne.

Rysunek nr 3. Biegunowa płata samolotu PZL.50 Jastrząb.


Turbulencja powstaje w warstwie przyściennej, gdy prędkość lub odległość od krawędzi natarcia są dostatecznie duże, wywołuje ona gwałtowne mieszanie się powolnych i szybkich cząstek płynu. W większości warstwy przyściennej prędkości stają się bardziej wyrównane, jednakże w pobliżu ścianki wytwarza się bardzo cienka podwarstwa laminarna, w której gradient prędkości jest nadzwyczaj wysoki. Podwarstwa ta określa czy powierzchnia jest „chropowata” czy „gładka” w sensie aerodynamicznym. Jeżeli nierówności powierzchni (np. główki nitów) są na tyle małe, że nie wychodzą ponad warstwę laminarną, to nie mają one wpływu na opór i powierzchnia może być uważana za aerodynamicznie gładką. Gdy nierówności są tak duże, że przebijają podwarstwę i sięgają warstwy turbulentnej, powstaje znaczny wzrost oporu tarcia i powierzchnia uważana jest za aerodynamicznie „chropowatą”. Jak wielka była wartość tego oporu? W przypadku skrzydła o konstrukcji metalowej standardowo przyjmuje się, że Cx tech wynosi 0,15 Cx min, jednak wszystko wskazuje na to, że wzrost oporu był znacznie większy, ponieważ wynikał z dwóch przyczyn. Oprócz wzrostu oporu tarcia skrzydła, następowało całkowite zaburzenie opływu laminarnego na dolnej części płata. Można teoretycznie przyjąć, że profil I.A.W. - 743 tracił swoje walory na skutek wadliwej konstrukcji płata. Keson Łosia miał konstrukcję opartą na patencie F. Misztala, pokrycie płata było nitowane, a łby nitów wpuszczane, dzięki temu uzyskano gładką powierzchnię z częściowym opływem laminarnym.

Zaburzenie opływu laminarnego na całej dolnej powierzchni płata odbierało Jastrzębiowi handicap, który w nieplanowany sposób przydarzył się Łosiowi.

Tabela nr 2


Tabela przedstawia następujące dane: pozycja druga - kąt natarcia, pozycja trzecia - wartość współczynnika oporu Cx przy nieskończonej rozpiętości płata, pozycja czwarta -C wartość współczynnika siły nośnej przy nieskończonej rozpiętości płata, pozycja piąta Cx' wartość współczynnika oporu skorygowana dla wyższych liczb Reynoldsa, pozycja szósta Cx'+Cx tech korekta współczynnika oporu o wzrost oporu wywołany względami technicznymi, pozycja siódma Cxi wartość współczynnika oporu indukcyjnego (S = 15,8, b = 9,7, ^ = 5,95), pozycja ósma – płat (S = 15,8, b = 9,7, ^ = 5,95) opór całkowity.

Całkowita siła aerodynamiczna na skrzydle jest wypadkową siły nośnej, oporu profilowego i oporu indukowanego. Opór profilowy wynika z działania płata nośnego, jako bryły o nieidealnym (niestety) kształcie opływowym i podlegającej działaniu lepkości przy poruszaniu się w płynie, ponadto przyjęliśmy, że dla klasycznych profili starszej generacji przy prędkościach rzędu Ma<0,4 wartości współczynnika Cx wyraźnie zależą od liczby Reynoldsa, dlatego postanowiliśmy uwzględnić ten efekt poprzez korektę związaną z faktem użytkowania samolotu przy liczbach Reynoldsa większych niż Re1= 700000. Liczba Reynoldsa odpowiadająca minimalnej prędkości lotu ustalonego w pobliżu ziemi (130 km/h) wynosi dla Jastrzębia 5800000. Dla konkretnych wartości Cx wylicza się poprawkę, wartość poprawki jest zawsze ujemna, dla tego skorygowana wartość – Cx' jest niższa.

Skrzydło o nieskończonej długości wytwarza przepływ, w którym zachowana jest określona energia cząstek powietrza opływających skrzydło. To samo zjawisko zachodzi na środku skrzydła o skończonej rozpiętości, natomiast na końcówkach skrzydeł wytwarzają się wiry spływowe, które wywołują dodatkowe odchylenie powietrza do dołu. W takim przepływie energia już się nie zachowuje i dla podtrzymania ruchu poziomego trzeba ją doprowadzić z zewnątrz. Ten rodzaj oporu nazywamy oporem indukowanym, oznaczamy go Cxi. Opór indukowany jest swego rodzaju podatkiem nałożonym przez naturę za przywilej latania. Skrzydła nie są w stanie unieść ciężaru samolotu bez tworzenia się wirów spływowych. Ich wytwarzanie się z kolei pociąga za sobą wydatkowanie energii, którą dostarczyć musi silnik samolotu. W 1919 roku Munk wykazał, że opór indukowany pojedynczego płata redukuje się do minimum, gdy prędkości odrzucania cząstek powietrza do dołu mają tę sama wartość wzdłuż całej rozpiętości skrzydła. Tę własność posiada „skrzydło eliptyczne” i w tym sensie jest skrzydłem doskonałym. Dzięki zastosowaniu skrzydeł o obrysie eliptycznym zmniejszono wielkość oporu indukowanego, mimo to był on przyczyną kłopotów Jastrzębia podczas zakrętów z małą prędkością lotu. Utrzymanie stałej wysokości, kiedy samolot jest przechylony dla zrównoważenia siły odśrodkowej wytwarzającej się w locie krzywoliniowym, wymaga takiego zwiększenia siły nośnej, by jej składowa pionowa była w stanie zrównoważyć ciężar samolotu.


Oznacza to również zwiększenie oporu indukowanego, a tym samym zwiększenie mocy silnika. Przy czym wzrost oporu będzie szczególnie duży wówczas, gdy w celu osiągnięcia znacznej siły wznoszenia samolot przechodzi do lotu o maksymalnych kątach natarcia. Ostatecznie następuje taki moment, w którym skrzydło jeszcze będzie w stanie zwiększać siłę nośną, ale mocy silnika nie starczy do pokonania zwiększającego się oporu. Liczby wyglądają następująco: przy maksymalnie dużych kątach natarcia siła oporu aerodynamicznego osiąga wielkość około 1/4 siły wznoszenia i jeżeli skrzydło może rozwijać siłę nośną sześciokrotnie przewyższającą ciężar samolotu, to do pokonania wzrastającego oporu będzie potrzebny silnik o ciągu 1,5 raza większym od ciężaru samolotu (współczynnik ciągu do ciężaru wynosi 1,5). Taki współczynnik w przypadku silnika tłokowego jest absolutnie nieosiągalny.

Jak wiadomo PZL.50 w zakręcie na małej prędkości miał tendencję do ślizgu na skrzydło. Rozbudowana mechanizacja płat (automatyczne sloty, klapy szczelinowe oraz klapa krokodylowa pod kadłubem) zwiększająca siłę nośną 2-2,5 krotnie, nie była w stanie temu zapobiegać, przypadłość tę błędnie wiązano ze zbyt małą mocą silnika. W tabeli nr 2 przedstawiamy wartość oporu indukowanego dla płata o wydłużeniu 5,95. W punkcie krytycznym opór indukowany płata jest bardzo wysoki (Cxi = 0,06237). Warto zauważyć, że tak wysoki opór indukowany daje płat o obrysie eliptycznym, w przypadku skrzydła trapezowego opór indukowany byłby o 20% wyższy. Wysoka wartość oporu indukowanego (która dodatkowo wzrastała w zakręcie) w połączeniu z niską wartością punktu krytycznego profilu IAW – 743 (13 stopni, Cz = 1,08, Cx = 0,1385) była przyczyną zwalania się na skrzydło.

To oczywiste, że najlepszym rozwiązaniem byłby montaż silnika o wyższej mocy, ale równie oczywistym był fakt, że takich silników nie posiadaliśmy, w tej sytuacji konstruktor musi brać pod uwagę wszystkie czynniki, zapewniając przy tym odpowiedni margines bezpieczeństwa. Nowe skrzydła były niezbędne, należało zwiększyć ich wydłużenie, zmniejszyć ciężar poprzez zastosowanie klasycznej konstrukcji dwudźwigarowej, poprawić jakość wykonania (staranne nitowanie, wygładzenie powierzchni), być może wprowadzić skręcenie aerodynamiczne płata w celu poprawienia zwrotności. Aerodynamika Jastrzębia wymagała krytycznej analizy już na etapie projektu, można przypuszczać, że ambitne zadanie przerosło możliwości ekipy Jakimiuka.

KADŁUB

Na pierwszy rzut oka kadłub Jastrzębia był aerodynamicznie poprawny. Zaprojektowano go zgodnie z najnowszymi trendami. Silnik Bristol Mercury VIII otrzymał nowoczesną osłonę typu NACA z klapkami regulującymi przepływ powietrza chłodzącego, która w połączeniu z dużym kołpakiem śmigła, bardzo efektywnie ograniczała opór czołowy silnika (średnica 1307 mm). Pokrycie kadłuba było nitowane z wpuszczanymi łebkami nitów. Stateczniki miały dobrane obrysy generujące mniejszy opór. Jednak podczas prób w locie stwierdzono usterki, których naprawa wymagała ingerencji w strukturę kadłuba. przede wszystkim powiększono wlot powietrza do gaźnika, który ograniczał dopływ powietrza do silnika, zmniejszając moc i osiągi samolotu. Poprawiono przejście skrzydło-kadłub w celu poprawienia opływu tylnej części kadłuba oraz powiększono i przeniesiono do góry statecznik poziomy. Tym sposobem wyeliminowano: drgania typu buffeting, niedostateczną skuteczność sterów oraz zlikwidowano przyczynę dławienia silnika.

Tabela 3- Zestawie danych dotyczących oporów samolotów wg R. Aleksandrowicz, W. Łucjanek, J. Martyniak. Załączniki do zbioru zadań z Mechaniki Lotu (PWN, Warszawa-Łódź 1962).


Tabela 3 przedstawia wartości minimalnego współczynnika oporu dla różnych rodzajów samolotów.
Wynika z niej, że współczynnik oporu minimalnego Jastrzębia powinien wynosić od 0,02 do 0,025. Dla porównania - współczynnik oporu wyścigowego samolotu Potez-53, wyglądający niczym miniatura Jastrzębia, sięgał wartości Cxmin = 0,0215, z tego 34% przypadało na skrzydła, 39% oporu dawał kadłub, stateczniki 9%, chłodnica oleju tylko 6%, strumień zaśmigłowy 12%. Aby w przybliżeniu określić wartość Cx Jastrzębia przyjmujemy, że relacje pomiędzy poszczególnymi składnikami są podobne. W związku z tym, jeżeli obliczony Cx płata wynosi 0,009349 (Tab. 2) to pozostałe współczynniki kształtują się następująco: Cx samolotu – 0,027497, Cx kadłuba – 0,010724, Cx usterzenia – 0,0024747, Cx chłodnicy – 0,001650.

Dysponując wartością współczynnika oporu możemy pokusić się na obliczenie prędkości maksymalnej. Brakuje jedynie sprawności śmigła. Andrzej Glass podaje, że w prototypie wypróbowano śmigła marek: Hamilton, Letov, Ratier można przyjąć, że sprawność tych śmigieł oscylowała wokół 80%.

Nr – moc rozporządzalna – 840 KM
n – sprawność śmigła - 0,8
S – powierzchnia nośna – 15,8 m
Cx – współczynnik oporu – 0,027497
q – gęstość powietrza - 0,812

Korzystamy ze wzoru Nr*n*736 = (S*V3*q*Cx)/2

Prędkość maksymalna liczona metodą mocy wynosi Vmax = 507,6 km/h. Po spełnieniu wszystkich teoretycznych przesłanek i wyeliminowaniu aerodynamicznych usterek, osiągnięcie prędkości maksymalnej było możliwe, jednak wymagało czasu. Bez wątpienia PZL.50 nie był samolotem optymalnie zaprojektowanym. Po usunięciu podstawowych usterek byłby co najwyżej maszyną przeciętną. Zwycięstwo w wielkich konfliktach zbrojnych zapewniał zwykle masowo produkowany i używany sprzęt przeciętnej jakości. Innego zdania jest Edward Malak, który zagadnienie przezbrojenia w nowy sprzęt ujmuje w następujący sposób: „Tym czasem względy obronne Polski narzucały sięganie po broń, co najmniej równą broni z zagranicy. Poprzestawanie na sprzęcie przeciętnym (choć nowym), w warunkach wyraźnej liczebnej przewagi państw w których upatrywano napastników, byłoby niejako ustawieniem wojsk polskich na z góry przegranej pozycji”. W kontekście katastrofy Wilka i Jastrzębia słowa E. Malaka nabierają szczególnej ironii.

Koniec części II.  

Czytaj dalej:
Dlaczego Jastrząb zawiódł?- część 3